Zahlenspiele
Wie wurde im alten China gerechnet?

Rechenmethode mit Rechenstäben im alten China
| Foto: © Dong Li Ba Jiu, Microfotos
Indisch-arabische Zahlen und Symbole wie +, -, × und ÷ wie wir sie heute in der Mathematik benutzen, verbreiteten sich in China erst in der ausgehenden Qing-Dynastie (1644-1911). Welche Rechenmethoden man zuvor in China benutzte und wie mit Schriftzeichen oder Rechenstäben die vier Grundrechenarten gehandhabt wurden, wird in diesem Artikel erläutert.
Rechenmethode mit chinesischen Schriftzeichen
Diese Methode basiert auf den Schriftzeichen für Grundzahlen und Zahleneinheiten. Man verwendete die Schriftzeichen 一 yī, 二 èr, 三 sān, 四 sì, 五 wǔ, 六 liù, 七 qī, 八 bā und 九 jiǔ für die Zahlen von 1-9, später auch noch die Zeichen 零 líng und 〇 für die Null. Dazu kamen 21 Schriftzeichen, welche die Position einer Ziffer innerhalb einer Zahl angeben, wie Einer (一yī ), Zehner (十 shí), Hunderter (百 bǎi), Tausender (千 qiān), Zehntausender (万 wàn), sowie Hundert Millionem (亿 yì), Billion (兆 zhào) und 京 jīng. Einer bis Zehntausender sind in Dezimalschritten abgestuft, von Zehntausend aufwärts jedoch existieren unterschiedliche Abstufungen. In der Antike vor der Qin-Dynastie (221 - 207 v. Chr.) wurden normalerweise Dezimalschritte angesetzt. Seit der Han-Dynastie (206 v. Chr. bis 220 n. Chr.) aber waren hauptsächlich zwei Handhabungen in Gebrauch: Zum einen gab es 10.000stellige Abstufungen, zum anderen erst 10.000 × 10.000 für 亿 yì (100.000.000), anschließend von 亿 yì zu 兆 zhào jeweils 100.000.000stellige Abstufungen.Seit alten Zeiten bis heute werden Zahlen unter Zehntausend in Form von „X-tausend (千) X-hundert (百) X-zehn (十) X“ angegeben. Was die Zahl Zehntausend überschritt, konnte je nach dem jeweils verwendeten Abstufungssystem unterschiedlich ausfallen. Rechnete man mit Dezimalschritten, so benutzte man die entsprechende Methode, so dass beispielsweise für die Zahl 534.863 die Schreibweise 五亿三万四千八百六十三 (5 yì 3 wàn 4 qiān 8 bǎi 6 shí 3). Setzte man jedoch zehntausendstellige Schritte an, so wurde für vielstellige Zahlen das Schema „X-tausend X-hundert X-zehn X“ zusammen mit den nötigen Zahleneinheiten verwendet. So wird etwa im mathematischen Werk Xu Gu Zhai Qi Suanfa (续古摘奇算法, Nachtrag zu den alten „Besonderen Rechenmethoden“) von Yang Hui (杨辉) aus dem 13. Jahrhundert die große Zahl 1.853.020.188.851 so geschrieben: 一兆八千五百三十亿二千一十八万八千八百五十一 (1 zhào 8 qiān 5 bǎi 30 yì 2 qiān 18 wàn 8 qiān 8 bǎi 5 shí 1). Hier wird ab 万wàn (10.000) in zehntausendstelligen Schritten gerechnet. Wenn wir nun alle Angaben für Zahleneinheiten weglassen und die fehlenden Stellen mit Nullen ausfüllen, so ergibt sich die Schreibweise 一八五三〇二〇一八八八五一, was der Zahl 1.853.020.188.851 im heute gebräuchlichen indisch-arabischen Zahlensystem exakt entspricht.
Die Bezeichnung von Zahlen mit chinesischen Schriftzeichen ist einfach und schlüssig. So wird etwa die Zahl 30 als 三十 sān shí angegeben und die Zahl 13 als 十三 shí sān (oder auch 一十三 yī shí sān). Es braucht also nur Begriffe für die Grundzahlen und die Zahleneinheiten. Ganz anders als bei den englischen Bezeichnungen „thirty“ und „thirteen“. Diese enthalten nicht nur zahlenfremde Elemente wie „ten“, „-ty“ und „thir-“, sondern setzen den Bestandteil „thir-“ für 3 sogar in beiden Begriffen an die Anfangsposition. In diesem Vergleich treten die Vorzüge der chinesischen Zahlenbezeichnungen klar zutage.
Rechenmethode mit Rechenstäben
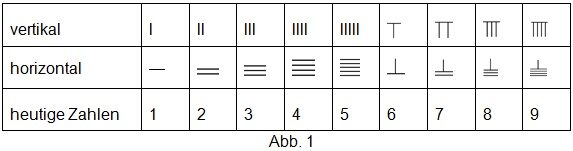
Rechenstäbe waren kleine Stäbchen aus Bambus, Holz oder anderen Materialien, mit denen die Zahlen ausgelegt wurden. Beim Rechnen verwendete man zwei Legeordnungen:In diesen Zeichen werden die Zahlen 1-5 jeweils mit der entsprechenden Anzahl Stäben dargestellt. Für die Zahlen von 6 bis 9 steht der oberste Stab für die Anzahl 5, während die im rechten Winkel darunter liegenden Stäbe angeben, um wie viel die Zahl 5 überschritten wird. Beim Rechnen werden alle Einer, Hunderter, Zehntausender etc. mit vertikalen Stäben, Zehner, Tausender, Hunderttausender etc. mit horizontalen Stäben dargestellt, so dass ein wechselnder Rhythmus von Horizontalen und Vertikalen entsteht. Nullstellen wurden als Leerstellen gehandhabt. Weil die Menschen im Altertum meist auf Sitzmatten am Boden saßen, galt die Regel, dass die Einer-Position beim rechten Knie anzulegen war. Um die Zahl 68.012 darzustellen, legte man die Stäbe folgendermaßen: — ll. Da das Rechnen mit Rechenstäben streng nach dem Dezimalsystem erfolgte, konnte dasselbe Zahlzeichen zur Bezeichnung verschiedener Zahleneinheiten verwendet werden, gleich wie beim heute üblichen indisch-arabischen Zahlensystem.
Die vier Grundrechenarten
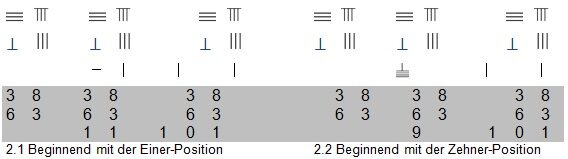
Im alten China wurden Berechnungen normalerweise mit Rechenstäben ausgeführt und mit Schriftzeichen notiert. Addition, Subtraktion, Multiplikation und Division wurden mithilfe von Schriftzeichen angegeben.Die alten chinesischen Standard-Werke der Mathematik erwähnen keine konkreten Methoden der Addition und Subtraktion. Dies mag damit zu tun haben, dass das Rechnen mit Rechenstäben höchst einfach war. Wir dürfen annehmen, dass es sich in etwa um dieselbe Methode handelte, wie wir sie heute beim schriftlichen Addieren und Subtrahieren verwenden. Nur wird es mit Rechenstäben noch einfacher, da sowohl mit der niederen als auch mit der höheren Stelle begonnen werden kann.
Im Folgenden ein Beispiel für zwei verschiedene Möglichkeiten, die Rechnung 38+63 auszuführen:
Im Altertum wurden Multiplikationen und Divisionen meist mit Rechenstäben durchgeführt. Dazu gehörte ein Merkspruch, das sogenannte „Neun-mal-Neun“ (九九口诀), denn das altchinesische Ein-mal-Eins begann mit „Neun mal Neun gibt Einundachtzig“. In verschiedenen Epochen wies weist der Spruch leichte Abweichung auf, doch die wichtigsten Aussagen von „Neun mal Neun gibt Einundachtzig“ (九九八十一) bis „Zwei mal Zwei gibt Vier“ (二二而四) blieben sich gleich. Im alten China konnte jedermann diesen einfachen Merkspruch auswendig.
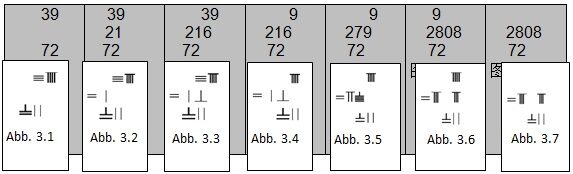
Will man beispielsweise 72×39 mit Rechenstäben errechnen, so legt man mit Rechenstäben die Zahlen in drei Reihen aus. In der Mitte kommt das Produkt zu stehen, oben und unten die beiden Faktoren, welche als „obere Zahl“ und „untere Zahl“ bezeichnet werden. Als erstes werden die Endziffer der unteren Zahl und die Anfangsziffer der oberen Zahl übereinander angeordnet (Abb. 3.1). Dann wird die Anfangsziffer 7 der unteren Zahl mit der Anfangsziffer 3 der oberen Zahl nach dem Merkspruch „Drei mal Sieben gibt Einundzwanzig“ multipliziert. Nun wird die Zahl 21 in der mittleren Reihe so ausgelegt, dass die Einer-Position 1 über den Faktor 7 zu stehen kommt (Abb. 3.2). Anschließend wird die 3 auch noch mit der der zweiten Stelle der unteren Zahl, nämlich der 2, nach dem Merkspruch „Zwei mal Drei gibt Sechs“ multipliziert und das Ergebnis 6 der mittleren Reihe beigefügt (Abb. 3.3). Da die Anfangsziffer 3 der oberen Zahl nun bereits mit allen Faktoren multipliziert worden ist, wird sie entfernt. Anschließend wird die untere Zahl nach rechts verschoben, so dass die Endziffer 2 und die nun als Anfangsziffer stehende obere Zahl 9 in derselben Spalte liegen (Abb. 3.4). Auf dieselbe Weise werden auch die beiden Positionen der unteren Zahl mit 9 multipliziert und der mittleren Reihe beigefügt. Dann wird der Faktor 9 entfernt und in der Mitte liegt das Ergebnis 2808 (Abb. 3.5-7).
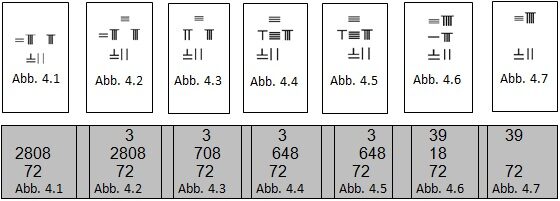
Beim Dividieren werden Dividende und Divisor in der mittleren und unteren Reihe angeordnet. Die obere Reihe für das Produkt bleibt zunächst leer. Als erstes wird der Divisor nach links verschoben, so dass er mit der Anfangsziffer der Dividende übereinstimmt. Falls in einer Spalte der Divisor grösser ist als die Dividende, wird der Divisor um eine Stelle nach rechts verschoben. So auch bei 2808÷72, wo die 72 unter die Ziffern 80 zu stehen kommt, weil 72 grösser ist als 28 (Abb. 4.1). Nun wird das vorläufige Produkt 3 in die obere Reihe gelegt, und zwar so, dass es mit der Einer-Position des Divisors in einer Spalte liegt (Abb. 4.2). Dann wird die Anfangsziffer 7 der Dividende nach dem Merkspruch „Drei mal Sieben gibt Einundzwanzig“ mit 3 multipliziert, und das Ergebnis 21 von der Zahl 28 (die zwei Positionen über der Ziffer 7 und der davorliegenden Ziffer) subtrahiert (Abb. 4.3). Anschließend wird nach dem Merkspruch „Zwei mal Drei gibt Sechs“ die Einer-Position 2 der Dividende mit 3 multipliziert und das Ergebnis 6 von der mittleren Reihe subtrahiert (Abb. 4.4). Nun wird die Dividende um eine Stelle nach rechts verschoben (Abb. 4.5). Die zweite Stelle des Produkts ergibt nun 9. Anschließend werden nach demselben Prinzip wie zuvor die 9 und das Produkt der Dividende von der mittleren Reihe subtrahiert. Am Ende geht die Division mit dem Produkt 39 auf (Abb. 4.6-7). Falls Restposten übrig sind, erhält man eine gemischte Zahl, wobei das Produkt die ganze Zahl und die Dividende zusammen mit dem Restposten als Nenner und Zähler übrigbleiben.
Anhand der obengenannten Methoden ließen sich im alten China alltägliche Rechenaufgaben bequem lösen. Damals wurden auch verschiedenfarbige Rechenstäbe verwendet, um positive und negative Zahlen zu kennzeichnen. Anhand von verschiedenen Auslegeordnungen konnten sogar Gleichungen und algebraische Formeln nach der heutigen Trennkoeffizient-Methode vorgenommen werden. Das machte die alte chinesische Mathematik nicht nur sehr praktisch, sondern ermöglichte auch eine hohe Entwicklung im Bereich der Algebra.