Mathematik zum Anfassen
Mathematische Experimente – Ein attraktiver Zugang zur Mathematik

Prof. Dr. Albrecht Beutelspacher, Direktor des Mathematikums
|
Foto: Rolf K. Wegst
Von Prof. Dr. Albrecht Beutelspacher
Vor über 200 Jahren entwarf der Schweizer Pädagoge Johann Heinrich Pestalozzi (1746-1827) die Vorstellung vom ganzheitlichen „Lernen mit Kopf Herz und Hand“. Diese Idee passt wie angegossen zu „Mathematik zum Anfassen“, bei der die Mathematik durch Experimente erschlossen wird, und zwar in dem Dreischritt Hand – Kopf – Herz:
- Zunächst stellt man etwas Reales her, in aller Regel mit einfachsten Materialien und ohne technischen Aufwand.
- In einem zweiten Schritt entdeckt man unerwartete Eigenschaften und erlebt ein großes mathematisches Potential. Man bildet Vorstellungen und erhält Einsichten.
- Die Erfahrung zeigt: Solche Experimente machen einfach Freude. Das liegt zunächst daran, dass jedes Experiment das Potential zu einem Erfolgserlebnis hat. Besonders viel Freude machen aber die Einsichten, die man alleine genießen, aber auch mit anderen teilen kann.
Dreieck
Dreiecke gehören zu den grundlegenden geometrischen Objekten. Sie bilden den einfachsten Figurentyp, der verschiedene Gestalten annehmen kann: Von Punkten und Gerade gibt es jeweils nur eine Sorte. Kreise kommen zwar groß und klein vor, sie sehen aber alle gleich aus. Bei den Dreiecken ist das nicht so, und daher gibt es auch ein Dreieck, welches das regelmäßigste ist: das gleichseitige Dreieck.Man kann ein gleichseitiges Dreieck aus einem rechteckigen Blatt Papier falten. Das geschieht in drei Schritten und einer kleinen Nacharbeit:
Zunächst faltet man das Blatt entlang der langen Symmetrieachse und klappt das Blatt wieder auf. Dann nimmt man eine Ecke und faltet sie auf die Mittellinie, aber so, dass an der benachbarten Ecke eine Spitze entsteht. Schließlich faltet man noch entlang der kurzen Seite des eben entstandenen Dreiecks und klappt schließlich die kleine überstehende Ecke ein.
 Abb. Dreieck 1, Dreieck 2, Dreieck 3
| Fotos: Albrecht Beutelspacher
Das Potenzial dieses kleinen Experiments zeigt sich, wenn wir uns fragen, wie man objektiv belegen könnte, dass das Dreieck tatsächlich gleichseitig ist und wir uns das nicht nur einbilden. Darauf gibt es viele Antworten auf unterschiedlichstem Niveau:
Abb. Dreieck 1, Dreieck 2, Dreieck 3
| Fotos: Albrecht Beutelspacher
Das Potenzial dieses kleinen Experiments zeigt sich, wenn wir uns fragen, wie man objektiv belegen könnte, dass das Dreieck tatsächlich gleichseitig ist und wir uns das nicht nur einbilden. Darauf gibt es viele Antworten auf unterschiedlichstem Niveau:
- Man könnte die drei Seiten des Dreiecks messen und überprüfen, ob sie gleich lang sind.
- Man könnte die Winkel messen und dabei herausfinden, dass diese 60 Grad betragen.
- Man könnte das Dreieck so falten, dass eine Kante auf einer anderen liegt. Die Faltlinie ist eine Symmetrieachse. Wenn man an einer zweiten Symmetrieachse faltet, hat man sich davon überzeugt, dass alle Kanten gleich lang sind.
- Wenn man das Experiment in der Klasse macht, hat jede Schülerin und jeder Schüler ein Dreieck und sie können diese miteinander vergleichen, indem sie diese aufeinander- bzw. aneinanderlegen. Das Aneinanderlegen führt zur Figurenlehre: Wenn man 2, 3, 4 oder 6 Dreiecke aneinanderlegt, kommt man automatisch zu Begriffen wie Raute, Trapez, Sechseck und deren Zerlegungen in Dreiecke.
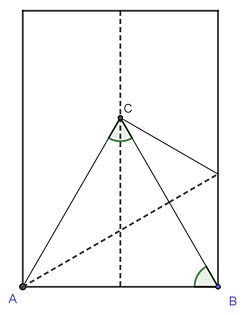 Abb. Dreiecksbeweis
| Fotos: Albrecht Beutelspacher
Abb. Dreiecksbeweis
| Fotos: Albrecht Beutelspacher
- Schließlich kann man die Gleichseitigkeit auch formal mathematisch durch einen Beweis begründen: In folgendem Bild sind die beiden ersten Faltungen eingezeichnet.
Sechseck
Kann man aus einem Dreieck ein Sechseck falten? Nichts leichter als das: Man faltet die Ecken zum Mittelpunkt des Dreiecks. Diesen kann man als den Schnittpunkt zweier Symmetrieachsen konstruieren.Auch die Sechsecke kann man aneinanderlegen und erhält ein Muster, das einer Bienenwabe gleicht. In der Tat legen Bienen ihre Waben als Parkettierung aus regelmäßigen Sechsecken.
Fünfeck und Pentagramm
Im Gegensatz zu Dreieck, Viereck, Sechseck ist ein reguläres Fünfeck nicht einfach vorzustellen, nicht einfach freihändig zu zeichnen und auch nicht einfach mit Zirkel und Lineal zu konstruieren.Für die folgende Konstruktion eines regulären Fünfecks braucht man einen Papierstreifen der etwa die Länge eines A4-Blattes hat und ca. 3 cm breit ist: Zunächst macht aus dem Streifen eine gewöhnliche Schleife – allerdings, ohne sie festzuziehen. Danach zieht man die Enden heraus, aber so, dass sie sich nicht wölben. Dann drückt man – im richtigen Moment – die Schleife zusammen, faltet die Enden nach hinten – und erhält ein perfektes Fünfeck.
Auch an diesem kleinen Objekt kann man interessante mathematische Beobachtungen machen. Man kann das Fünfeck so halten, dass man darauf eine Art Segelboot erkennt. Die Oberkante des Schiffrumpfes ist parallel zur Unterkante, weil es sich um die zwei Kanten des Papierstreifens handelt. In mathematischer Sprache ist diese Oberkante eine Diagonale des Fünfecks. Das heißt, dass bei einem regulären Fünfeck jede Diagonale parallel zu einer Seite ist.
 Abb. Fünfeck 2, Fünfeck 3
| Fotos: Albrecht Beutelspacher
Bei dem gefalteten Fünfeck erkennt man ein Stück einer zweiten Diagonalen. Wenn man alle Diagonalen einzeichnet, erhält man einen Stern, das berühmte Pentagramm. Dieses spielt auch in der Mathematik eine wichtige Rolle, denn an ihm haben die griechischen Mathematiker vor 2500 Jahren irrationale Zahlen entdeckt: Hippasos von Metapont (ca. 500 v. Chr.) konnte beweisen, dass der Schnittpunkt zweier Diagonalen jede der Diagonalen in einem Verhältnis teilt, das keine Bruchzahl ist.
Abb. Fünfeck 2, Fünfeck 3
| Fotos: Albrecht Beutelspacher
Bei dem gefalteten Fünfeck erkennt man ein Stück einer zweiten Diagonalen. Wenn man alle Diagonalen einzeichnet, erhält man einen Stern, das berühmte Pentagramm. Dieses spielt auch in der Mathematik eine wichtige Rolle, denn an ihm haben die griechischen Mathematiker vor 2500 Jahren irrationale Zahlen entdeckt: Hippasos von Metapont (ca. 500 v. Chr.) konnte beweisen, dass der Schnittpunkt zweier Diagonalen jede der Diagonalen in einem Verhältnis teilt, das keine Bruchzahl ist. Abb. Pop-up Dodekaeder
| Fotos: Albrecht Beutelspacher
Die Überlieferung sagt, dass Hippasos das am Dodekaeder entdeckt habe. Das Dodekaeder ist ein Körper, der aus zwölf regulären Fünfecken besteht. Wir können uns heute das Dodekaeder auf vielfältige Weise vor Augen führen. Ein spektakuläres Experiment besteht darin, dass man zwei „halbe“ Dodekaeder aus dicker Pappe ausschneidet, die Verbindungskanten einritzt, beide Teile aufeinanderlegt, mit einem Gummiring verbindet – und dann loslässt!
Abb. Pop-up Dodekaeder
| Fotos: Albrecht Beutelspacher
Die Überlieferung sagt, dass Hippasos das am Dodekaeder entdeckt habe. Das Dodekaeder ist ein Körper, der aus zwölf regulären Fünfecken besteht. Wir können uns heute das Dodekaeder auf vielfältige Weise vor Augen führen. Ein spektakuläres Experiment besteht darin, dass man zwei „halbe“ Dodekaeder aus dicker Pappe ausschneidet, die Verbindungskanten einritzt, beide Teile aufeinanderlegt, mit einem Gummiring verbindet – und dann loslässt!