Apčiuopiama matematika
Matematiniai eksperimentai – patrauklus būdas mokytis matematikos

Prof. dr. Albrecht Beutelspacher, „Mathematikum“ direktorius | Foto: Rolf K. Wegst
Prof. dr. Albrecht Beutelspacher
Daugiau kaip prieš 200 metų šveicarų pedagogas Johannas Heinrichas Pestalozzi (1746–1827) sukūrė koncepciją apie visapusišką „proto, širdies ir rankos lavinimą“. Ši idėja idealiai pritaikoma „čiupinėjant matematiką“, kai su matematika susipažįstama atliekant eksperimentus, t. y. šiais trimis etapais: ranka – galva – širdis:
- Pirmiausia sukuriamas koks nors realus objektas, dažnai iš paprasčiausių medžiagų ir taikant nesudėtingą technologiją.
- Antrajame etape atrandamos netikėtos savybės ir susipažįstama su dideliu matematiniu potencialu. Atsiranda supratimas ir daromos įžvalgos.
- Patirtis rodo, kad tokie eksperimentai tiesiog teikia džiaugsmą. Taip atsitinka pirmiausia todėl, kad labai tikėtina, jog kiekvienas eksperimentas pavyks. O daugiausia džiaugsmo sukelia atradimai, kuriais galima ir džiaugtis vienam, ir pasidalyti su kitais.
Trikampis
Trikampiai priskiriami prie elementarių geometrinių objektų. Trikampiai – tai paprasčiausios figūros, galinčios įgauti įvairias formas (palyginimui – taškai ir tiesės gali būti tik vienos rūšies). Tiesa, apskritimai gali būti dideli ir maži, tačiau jie visi atrodo vienodi. Trikampiai nėra vienodi, bet galima išskirti vieną trikampį, kuris yra taisyklingiausias – tai lygiakraštis trikampis.Lygiakraštį trikampį galima išlankstyti iš stačiakampio popieriaus lapo. Tai galima padaryti trimis veiksmais ir įdėjus šiek tiek papildomo darbo:
pirmiausia lapas išilgai sulenkiamas pagal simetrijos ašį ir vėl ištiesinamas. Tuomet paimamas vienas kampas ir lenkiamas prie centrinės linijos, bet lenkiamas tokiu būdu, kad gretimas kampas būtų smailus. Galiausiai dar lenkiama pagal trumpąją atsiradusio trikampio kraštinę ir užlenkiamas mažas išsikišęs trikampėlis.
 Pav. 1 trikampis, 2 trikampis, 3 trikampis
| Albrechto Beutelspacherio nuotr.
Šio paprasto eksperimento prasmė paaiškėja, kai iškeliame klausimą, kaip būtų galima objektyviai įrodyti, kad trikampis iš tiesų yra lygiakraštis, o ne tik mums atrodo, kad jis toks yra. Į šį klausimą galima atsakyti įvairiausiais būdais:
Pav. 1 trikampis, 2 trikampis, 3 trikampis
| Albrechto Beutelspacherio nuotr.
Šio paprasto eksperimento prasmė paaiškėja, kai iškeliame klausimą, kaip būtų galima objektyviai įrodyti, kad trikampis iš tiesų yra lygiakraštis, o ne tik mums atrodo, kad jis toks yra. Į šį klausimą galima atsakyti įvairiausiais būdais:
- Galima išmatuoti visas tris trikampio kraštines ir patikrinti, ar jos vienodo ilgio.
- Galima išmatuoti kampus ir tokiu būdu sužinoti, ar juos sudaro 60 laipsnių.
- Galima trikampį sulankstyti taip, kad viena kraštinė bus užklota ant kitos. O lankstymo linija bus simetriška vidurio ašis. Jei perlenksime trikampį per kitą simetrišką vidurio liniją, įsitikinsime, kad visos kraštinės yra vienodos.
- Jei šį eksperimentą atliekame klasėje, visi mokiniai turi po trikampį ir gali juos tarpusavyje palyginti, sudėdami vieną šalia kito ar vieną ant kito. Sudėję trikampius vieną šalia kito susipažinsite su geometrinėmis figūromis: jei 2, 3, 4 ar 6 trikampius sudėsime vieną šalia kito, neišvengiamai susidursime su kai kuriomis sąvokomis, kaip antai rombas, trapecija, šešiakampis, ir jų išskaidymu į trikampius.
- Galiausiai kraštinių lygybę galima pagrįsti matematiškai, t. y. pateikus įrodymą: žr. šiame paveikslėlyje pateikiamus abu pirmuosius lankstinius.
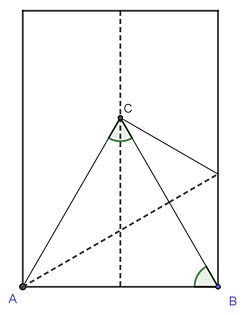 Pav. trikampio įrodymas
| Albrechto Beutelspacherio nuotr.
Kadangi sulenkta vidurinė linija yra simetriška ašis, vadinasi AC = BC. Antrajame lankstinyje B sutampa su C, vadinasi, AB = AC. Todėl trikampis DABC yra lygiakraštis. Toliau galima daryti visas kitas išvadas.
Pav. trikampio įrodymas
| Albrechto Beutelspacherio nuotr.
Kadangi sulenkta vidurinė linija yra simetriška ašis, vadinasi AC = BC. Antrajame lankstinyje B sutampa su C, vadinasi, AB = AC. Todėl trikampis DABC yra lygiakraštis. Toliau galima daryti visas kitas išvadas.
Šešiakampis
Ar galima iš trikampio išlankstyti šešiakampį? Paprasčiau nebūna: pakanka kampus užlenkti į trikampio centrinį tašką. Centrinis taškas bus dviejų simetriškų ašių susikirtimo taškas.Šešiakampius taip pat galima sudėti vieną šalia kito – tuomet susidarys raštas, panašus į bičių korį. Bitės iš tikrųjų korio akutes konstruoja kaip parketą iš taisyklingų šešiakampių.
Penkiakampis ir pentagrama
Priešingai negu trikampį, keturkampį ar šešiakampį, taisyklingą penkiakampį nėra paprasta įsivaizduoti, nubraižyti ranka ir sukonstruoti netgi naudojantis skriestuvu bei liniuote.Norint sukonstruoti taisyklingą penkiakampį reikės popieriaus juostelės, kuri yra maždaug A4 formato lapo ilgio ir 3 cm pločio. Pirmiausia suriškite iš juostelės paprastą mazgą, bet jo nesuveržkite. Patraukite abu galus, stengdamiesi išlaikyti juos tiesius ir lygius. O tada, nutaikę tinkamą momentą, suplokite mazgą, užlenkite išsikišusius galus ir štai – tobulas penkiakampis.
Su šiuo nedideliu objektu taip pat galite atrasti įdomių matematinių paralelių. Galima laikyti penkiakampį rankoje taip, kad jis būtų panašus į savotišką burinį laivelį. Viršutinė laivo korpuso dalis yra lygiagreti apatinei korpuso daliai, nes šios dalys yra popieriaus juostelės kraštai. Kalbant matematikų kalba, šis viršutinis kraštas yra penkiakampio įstrižainė. Vadinasi, kiekviena taisyklingo penkiakampio įstrižainė yra lygiagreti jo šonui.
 Pav. 2 penkiakampis, 3 penkiakampis
| Albrechto Beutelspacherio nuotr.
Sulankstytame penkiakampyje matyti dalis antros įstrižainės. Jei pažymėsite visas įstrižaines, nubraižysite žvaigždę, garsiąją pentagramą. Matematikoje ji taip pat atlieka reikšmingą vaidmenį, nes ja naudodamiesi graikų matematikai prieš 2500 metų atrado iracionaliuosius skaičius: Hipasas Metapontietis (apie 500 m. prieš Kristų) įrodė, kad dviejų įstrižainių susikirtimo taškas kiekvieną įstrižainę padalija tokiu santykiu, kurio negalima išreikšti sveikuoju skaičiumi.
Pav. 2 penkiakampis, 3 penkiakampis
| Albrechto Beutelspacherio nuotr.
Sulankstytame penkiakampyje matyti dalis antros įstrižainės. Jei pažymėsite visas įstrižaines, nubraižysite žvaigždę, garsiąją pentagramą. Matematikoje ji taip pat atlieka reikšmingą vaidmenį, nes ja naudodamiesi graikų matematikai prieš 2500 metų atrado iracionaliuosius skaičius: Hipasas Metapontietis (apie 500 m. prieš Kristų) įrodė, kad dviejų įstrižainių susikirtimo taškas kiekvieną įstrižainę padalija tokiu santykiu, kurio negalima išreikšti sveikuoju skaičiumi. Pav. Išsiplečiantis dodekaedras
| Albrechto Beutelspacherio nuotr.
Legenda byloja, kad Hipasas šį atradimą padarė su dodekaedru. Dodekaedras – tai briaunainis, sudarytas iš dvylikos taisyklingų penkiakampių. Šiandien su dodekaedrais galime susipažinti įvairiausiais būdais. Taip pat atlikę įspūdingą eksperimentą, kurio metu du „dalinius“ dodekaedrus iškerpame iš storo kartono, įpjauname jungiamąsias kraštines, sudedame abi dalis vieną ant kitos, sujungiame jas gumos žiedeliu ir paleidžiame!
Pav. Išsiplečiantis dodekaedras
| Albrechto Beutelspacherio nuotr.
Legenda byloja, kad Hipasas šį atradimą padarė su dodekaedru. Dodekaedras – tai briaunainis, sudarytas iš dvylikos taisyklingų penkiakampių. Šiandien su dodekaedrais galime susipažinti įvairiausiais būdais. Taip pat atlikę įspūdingą eksperimentą, kurio metu du „dalinius“ dodekaedrus iškerpame iš storo kartono, įpjauname jungiamąsias kraštines, sudedame abi dalis vieną ant kitos, sujungiame jas gumos žiedeliu ir paleidžiame!